将详细推导出看跌期权的定价公式，并在此基础上推导出看涨看跌期权平价定理。理解这两个定理对于掌握期权定价和套利策略至关重要。 看涨看跌期权平价定理揭示了在没有套利机会的市场中，看涨期权和看跌期权的价格之间存在着确定的关系。这个关系并不依赖于具体的定价模型，只依赖于期权的标的资产价格、执行价格、到期时间以及无风险利率。 而看跌期权的定价公式则可以帮助我们根据市场信息计算看跌期权的理论价格，并评估其投资价值。

期权的基本概念

在深入推导之前，我们先明确一些基本概念。期权是一种赋予持有人在未来特定日期（到期日）以特定价格（执行价格）买卖标的资产的权利，而非义务。看涨期权（Call Option）赋予持有人在到期日以执行价格买入标的资产的权利；看跌期权（Put Option）赋予持有人在到期日以执行价格卖出标的资产的权利。 期权合约的价值会随着标的资产价格、到期时间、波动率以及无风险利率的变化而波动。 这些因素都将被纳入到我们的定价公式中。

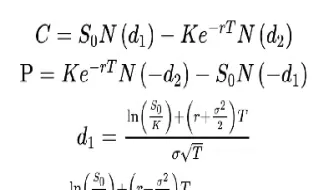
看涨看跌期权平价定理的推导

假设存在一种无风险投资组合，该投资组合由以下资产构成：一份看涨期权(C)，一份看跌期权(P)，以及在到期日卖出股票的承诺。 让我们考虑在到期日T时的两种情况：
1. 标的资产价格S_T ≥ X (X为执行价格): 在这种情况下，看涨期权将被执行，持有人将以X的价格买入标的资产，并立即以S_T的价格卖出，获得S_T - X 的利润。看跌期权到期失效，价值为0. 该投资组合的价值为 S_T - X.
2. 标的资产价格S_T < X: 在这种情况下，看涨期权到期失效，价值为0。持有人将执行看跌期权，以X的价格卖出标的资产，获得X - S_T 的利润。该投资组合的价值为 X - S_T.
无论哪种情况，该投资组合在到期日的价值都等于 X。这表明，该投资组合的价值是一个确定的值。根据无套利原则，该投资组合的现值等于其未来确定价值的现值。 我们可以建立以下等式：
C + P - S₀e^-rT = Xe^-rT
其中：
C：看涨期权价格
P：看跌期权价格
S₀：标的资产当前价格
X：执行价格
r：无风险利率
T：到期时间
e：自然对数的底数

通过整理上述公式，我们得到看涨看跌期权平价定理：
C + P = S₀ + Xe^-rT
这个公式表明，在没有套利机会的市场中，看涨期权和看跌期权的价格之和等于标的资产现值加上执行价格的折现值。

看跌期权定价公式的推导

利用看涨看跌期权平价定理，我们可以推导出看跌期权的定价公式。 从平价定理公式中，我们可以解出看跌期权的价格：
P = S₀ + Xe^-rT - C
这个公式表明，看跌期权的价格取决于标的资产的价格、执行价格、到期时间、无风险利率以及看涨期权的价格。 如果我们已知看涨期权的价格(C)，就可以通过这个公式计算出看跌期权的价格(P)。

Black-Scholes 模型与看跌期权定价

虽然上述推导基于无套利原则，但它并没有给出看涨期权价格(C)的具体计算方法。 Black-Scholes 模型提供了一种计算欧式期权价格的理论模型，其公式考虑了标的资产的波动率、时间以及无风险利率。 将Black-Scholes 模型的看涨期权定价公式代入上述看跌期权定价公式，我们可以得到一个基于Black-Scholes 模型的看跌期权定价公式。 Black-Scholes 模型的推导较为复杂，涉及到随机微积分和伊藤引理，这里不再赘述。

实际应用与局限性

看涨看跌期权平价定理和看跌期权定价公式在实际金融市场中具有广泛的应用。 交易员可以使用这些公式来评估期权价格的合理性，识别套利机会，并构建复杂的期权交易策略。 这些公式也存在一些局限性。 这些公式假设市场是完全有效的，没有交易成本，也没有套利机会。 Black-Scholes 模型的假设，例如标的资产价格服从几何布朗运动，在实际市场中可能并不完全成立。 在实际应用中，需要根据市场情况进行调整和修正。

推导了看跌期权定价公式，并在此基础上推导了看涨看跌期权平价定理。 这两个定理是期权定价理论中的重要组成部分，它们揭示了看涨期权和看跌期权价格之间的内在联系，并为期权定价和风险管理提供了重要的工具。 虽然这些公式在实际应用中存在一些局限性，但它们仍然是理解和分析期权市场的重要基础。